미션 프로토콜

The mission sub-protocol allows a GCS or developer API to exchange mission (flight plan), geofence and safe point information with a drone/component.

The protocol covers:

• Operations to upload, download and clear missions, set/get the current mission item number, and get notification when the current mission item has changed.
• Message type(s) and enumerations for exchanging mission items.
• Mission Items ("MAVLink commands") that are common to most systems.

The protocol supports re-request of messages that have not arrived, which allows missions to be reliably transferred over a lossy link.

Mission Types

MAVLink 2 supports three types of "missions": flight plans, geofences and rally/safe points. The protocol uses the same sequence of operations for all types (albeit with different types of Mission Items). The mission types must be stored and handled separately/independently.

Mission protocol messages include the type of associated mission in the mission_type field (a MAVLink 2 message extension). The field takes one of the MAV_MISSION_TYPE enum values: MAV_MISSION_TYPE_MISSION, MAV_MISSION_TYPE_FENCE, MAV_MISSION_TYPE_RALLY.

INFO

MAVLink 1 supports only "regular" flight-plan missions (this is implied/not explicitly set).

Mission Items (MAVLink Commands)

Mission items for all the mission types are defined in the MAV_CMD enum.

INFO

MAV_CMD is used to define commands that can be used in missions ("mission items") and commands that can be sent outside of a mission context (using the Command Protocol). Some MAV_CMD can be used with both mission and command protocols. Not all commands/mission items are supported on all systems (or for all flight modes).

The items for the different types of mission are identified using a simple name prefix convention:

• Flight plans:
  • NAV commands (MAV_CMD_NAV_*) for navigation/movement (e.g. MAV_CMD_NAV_WAYPOINT, MAV_CMD_NAV_LAND)
  • DO commands (MAV_CMD_DO_*) for immediate actions like changing speed or activating a servo (e.g. MAV_CMD_DO_CHANGE_SPEED).
  • CONDITION commands (MAV_CMD_CONDITION_*) for changing the execution of the mission based on a condition - e.g. pausing the mission for a time before executing next command (MAV_CMD_CONDITION_DELAY).
• Geofence mission items:
  • Prefixed with MAV_CMD_NAV_FENCE_ (e.g. MAV_CMD_NAV_FENCE_RETURN_POINT).
• Rally point mission items:
  • There is just one rally point MAV_CMD: MAV_CMD_NAV_RALLY_POINT.

Mission items (MAV_CMD) are transmitted/encoded in MISSION_ITEM_INT messages. This message includes fields to identify the particular mission item (command id) and up to 7 command-specific optional parameters.

Field Name	Type	Values	Description
command	uint16_t	MAV_CMD	Command id, as defined in MAV_CMD.
param1	float		Param #1.
param2	float		Param #2.
param3	float		Param #3.
param4	float		Param #4.
param5 (x)	int32_t		X coordinate (local frame) or latitude (global frame) for navigation commands (otherwise Param #5).
param6 (y)	int32_t		Y coordinate (local frame) or longitude (global frame) for navigation commands (otherwise Param #6).
param7 (z)	float		Z coordinate (local frame) or altitude (global - relative or absolute, depending on frame) (otherwise Param #7).

The first four parameters (shown above) can be used for any purpose - this depends on the particular command. The last three parameters (x, y, z) are used for positional information in MAV_CMD_NAV_* commands, but can be used for any purpose in other commands.

The remaining message fields are used for addressing, defining the mission type, specifying the reference frame used for x, y, z in MAV_CMD_NAV_* messages, etc.:

Field Name	Type	Values	Description
target_system	uint8_t		System ID
target_component	uint8_t		Component ID
seq	uint16_t		Sequence number for item within mission (indexed from 0).
frame	uint8_t	MAV_FRAME	| | frame | uint8_t | MAV_FRAME | The coordinate system of the waypoint. ArduPilot and PX4 both only support global frames in MAVLink commands (local frames may be supported if the same command is sent via the command protocol).
mission_type	uint8_t	MAV_MISSION_TYPE	Mission type.
current	uint8_t	false:0, true:1	When downloading, whether the item is the current mission item.
autocontinue	uint8_t		Autocontinue to next waypoint when the command completes.

Message/Enum Summary

The following messages and enums are used by the service.

Message	Description
MISSION_REQUEST_LIST	Initiate mission download from a system by requesting the list of mission items.
MISSION_COUNT	Send the number of items in a mission. This is used to initiate mission upload or as a response to MISSION_REQUEST_LIST when downloading a mission.
MISSION_REQUEST_INT	Request mission item data for a specific sequence number be sent by the recipient using a MISSION_ITEM_INT message. Used for mission upload and download.
MISSION_ITEM_INT	Message encoding a mission item/command (defined in a MAV_CMD). Used for mission upload and download.
MISSION_ACK	Acknowledgment message when a system completes a mission operation (e.g. sent by autopilot after it has uploaded all mission items). The message includes a MAV_MISSION_RESULT indicating either success or the type of failure.
MISSION_CURRENT	Message containing the current mission item sequence number. This is streamed and also emitted when the current mission item is set/changed.
MISSION_SET_CURRENT	Set the current mission item by sequence number (continue to this item on the shortest path).
STATUSTEXT	Sent to notify systems when a request to set the current mission item fails.
MISSION_CLEAR_ALL	Message sent to clear/delete all mission items stored on a system.
MISSION_ITEM_REACHED	Message emitted by system whenever it reaches a new waypoint. Used to monitor progress.

Command	Description
MAV_CMD_DO_SET_MISSION_CURRENT	Set current mission item and optionally reset mission counter. Supersedes MISSION_SET_CURRENT.

Enum	Description
MAV_MISSION_TYPE	Mission type for message (mission, geofence, rallypoints).
MAV_MISSION_RESULT	Used to indicate the success or failure reason for an operation (e.g. to upload or download a mission). This is carried in a MISSION_ACK.
MAV_FRAME	Co-ordinate frame for position/velocity/acceleration data in the message.
MAV_CMD	Mission Items (and MAVLink commands) sent in MISSION_ITEM_INT.

Deprecated Types: MISSION_ITEM

The legacy version of the protocol also supported MISSION_REQUEST for requesting that a mission be sent as a sequence of MISSION_ITEM messages.

Both MISSION_REQUEST and MISSION_ITEM messages are now deprecated, and should no longer be sent. If MISSION_REQUEST is recieved the system should instead respond with MISSION_ITEM_INT items (as though it received MISSION_REQUEST_INT).

Frames & Positional Information

By convention, mission items use param5, param6, param7 for positional information when needed (and otherwise as "free use" parameters). The table below shows that the positional parameters can be local (x, y, z), global (latitude, longitude, altitude), and also the data type used to store the parameters in the MISSION_ITEM_INT message.

param	type	Local	Global
param5	int32_t	x	Latitude
param6	int32_t	y	Longitude
param7	float	z	Altitude (global - relative or absolute)

The co-ordinate frame of positional parameters is defined in the MISSION_ITEM_INT.frame field using a MAV_FRAME value.

The global frames are prefixed with MAV_FRAME_GLOBAL_*. Mission items should use frame variants that have the suffix _INT: e.g. MAV_FRAME_GLOBAL_RELATIVE_ALT_INT, MAV_FRAME_GLOBAL_INT, MAV_FRAME_GLOBAL_TERRAIN_ALT_INT. When using these frames, latitude and longitude values must be encoded by multiplying the degrees by 1E7 (e.g. the latitude 69.69000000 would be sent as 69.69000000x1E7 = 696900000). Using int32 of degrees * 10^7 has higher resolution than could be achieved with single floating point.

A number of local frames are also specified. Local frame position values that are sent in integer field parameters must be encoded as position in meters x 1E4 (e.g. 5m would be encoded and sent as 50000). If sent in messages float parameter fields the value should be sent as-is.

INFO

Don't use the non-INT global frames in mission items (e.g. MAV_FRAME_GLOBAL_RELATIVE_ALT). These are intended to be used with messages that have float fields for positional information, e.g.: MISSION_ITEM (deprecated), COMMAND_LONG. If these frames are used, position values should be sent unencoded (i.e. no need to multiply by 1E7).

INFO

As above, in theory if a global non-INT frame variant is set for a MISSION_ITEM_INT the position value should be sent as-is (not encoded). This will result in the value being rounded when it is sent in the integer value, which will make the value unusable. In practice, many systems will assume you have encoded the value, but you should test this for your particular flight stack. Better just to use the correct frames!

WARNING

Don't use MAV_FRAME_MISSION for mission items that contain positional data; this does not correspond to any particular real frame, and so will be ambiguous. MAV_FRAME_MISSION should be used for mission items that use params5 and param6 for other purposes.

Param 5, 6 For Non-Positional Data

Param5, param6, param7 may also be used for non-positional information. In this case the MISSION_ITEM_INT.frame should be set to MAV_FRAME_MISSION (this is equivalent to say "the frame data is irrelevant").

As param5 and param6 are sent in integer fields, generally you should design mission items/MAV_CMDs such that these only include integer data (and are sent as-is/unscaled). If these must be used for real numbers and scaling is required, then this must be noted in the mission item itself.

Operations

This section defines all the protocol operations.

Detecting Mission/Plan Changes

Mission upload and download can be expensive operations, in particular for large missions. A GCS can avoid unnecessary uploads and downloads by first checking whether it has a matching id(s) for the corresponding plan on the vehicle.

The current id for different parts of the plan are streamed in MISSION_CURRENT message, using the appropriately named fields: mission_id, fence_id, rally_points_id. These values are 0 if there is no plan uploaded, or if detecting plan changes is not supported by the flight stack.

The IDs are generated by the flight stack when a new mission, rally point, or geofence, is uploaded to the vehicle (at which point it also starts publishing the value in MISSION_CURRENT). MAVLink puts no particular requirements on how the "opaque_id" values are calculated by the flight stack (this is why they are named "opaque"). The only expectation is that the scheme used makes it unlikely that the GCS will incorrectly determine that it has a matching plan (a flight stack might use file hashes, plan checksums, pseudo-random numbers, or some other technique).

On upload, the generated ID is sent to the GCS in the final part of the upload sequence in the MISSION_ACK.opaque_id field. On download, the stored ID is sent to the GCS in the MISSION_COUNT.opaque_id field.

The GCS should store the value of the ID from the flight stack as the "current id" for whatever part of the plan was uploaded/download. It can then monitor MISSION_CURRENT, and check its cached values against the current plan ids to determine whether it has a matching mission, or needs to download the mission from the vehicle.

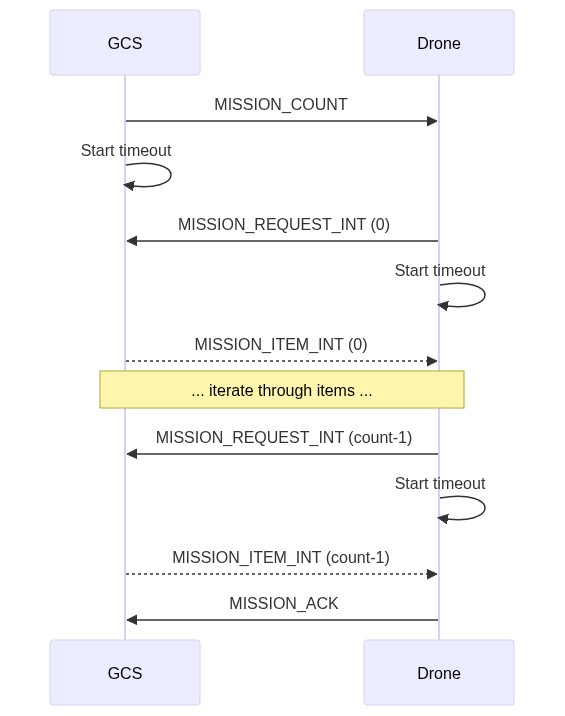
Upload a Mission to the Vehicle

The diagram below shows the communication sequence to upload a mission to a drone (assuming all operations succeed).

WARNING

Mission update must be robust! A new mission should be fully uploaded and accepted before the old mission is replaced/removed.

TIP

Mission upload/download can be bandwidth intensive and time consuming. Check for plan changes before uploading (or downloading) a mission.

In more detail, the sequence of operations is:

1. GCS sends MISSION_COUNT including the number of mission items to be uploaded (count).
   • A timeout must be started for the GCS to wait on the response from Drone (MISSION_REQUEST_INT).
2. Drone receives message and responds with MISSION_REQUEST_INT requesting the first mission item (seq==0).
   • A timeout must be started for the Drone to wait on the MISSION_ITEM_INT response from GCS.
3. GCS receives MISSION_REQUEST_INT and responds with the requested mission item in a MISSION_ITEM_INT message.
4. Drone and GCS repeat the MISSION_REQUEST_INT/MISSION_ITEM_INT cycle, iterating seq until all items are uploaded (seq==count-1).
5. After receiving the last mission item the drone responds with MISSION_ACK with the type of MAV_MISSION_ACCEPTED indicating mission upload completion/success.
   • The drone should set the new mission to be the current mission, discarding the original data.
   • The drone considers the upload complete.
6. GCS receives MISSION_ACK containing MAV_MISSION_ACCEPTED to indicate the operation is complete.
   • The GCS should store MISSION_ACK.opaque_id (the current id of the uploaded plan) and can use it later to check for plan changes.

Notes:

• A timeout is set for every message that requires a response (e.g. MISSION_REQUEST_INT). If the timeout expires without a response being received then the request must be resent.
• Mission items must be received in order. If an item is received out-of-sequence the expected item should be re-requested by the vehicle (the out-of-sequence item is dropped).
• An error can be signaled in response to any request using a MISSION_ACK message containing an error code. This must cancel the operation and restore the mission to its previous state. For example, the drone might respond to the MISSION_COUNT request with a MAV_MISSION_NO_SPACE if there isn't enough space to upload the mission.
• The sequence above shows the mission items packaged in MISSION_ITEM_INT messages. Protocol implementations must also support MISSION_ITEM and MISSION_REQUEST in the same way.
• Uploading an empty mission (MISSION_COUNT is 0) has the same effect as clearing the mission.

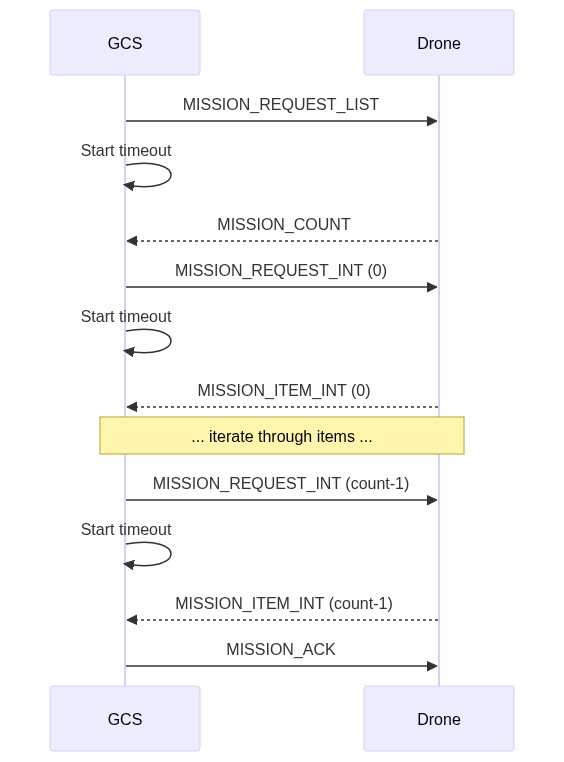
Download a Mission from the Vehicle

INFO

Mission upload/download can also be bandwidth intensive and time consuming. Check for plan changes before downloading (or uploading) a mission.

The diagram below shows the communication sequence to download a mission from a drone (assuming all operations succeed).

The sequence is similar to that for uploading a mission. The main difference is that the client (e.g. GCS) sends MISSION_REQUEST_LIST, which triggers the autopilot to respond with the current count of items (MISSION_COUNT). This starts a cycle where the GCS requests mission items, and the drone supplies them.

Note:

• The MISSION_COUNT.opaque_id is the stored ID of the part of the plan that is being uploaded from the vehicle. This should be stored by the GCS so that it can later check that its plan matches that on the vehicle.
• A timeout is set for every message that requires a response (e.g. MISSION_REQUEST_INT). If the timeout expires without a response being received then the request must be resent.
• Mission items must be received in order. If an item is received out-of-sequence the expected item should be re-requested by the GCS (the out-of-sequence item is dropped).
• An error can be signaled in response to any request using a MISSION_ACK message containing an error code. This must cancel the operation.
• The sequence above shows the mission items packaged in MISSION_ITEM_INT messages. Protocol implementations must also support MISSION_ITEM and MISSION_REQUEST in the same way.

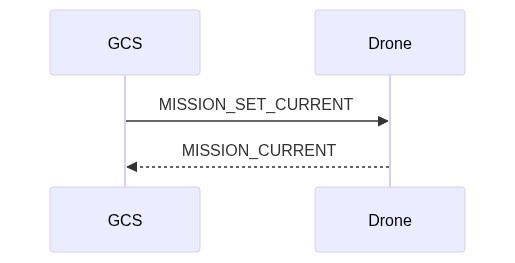
Set Current Mission Item

The diagram below shows the communication sequence to set the current mission item.

In more detail, the sequence of operations is:

1. GCS/App sends MAV_CMD_DO_SET_MISSION_CURRENT (or MISSION_SET_CURRENT), specifying the new sequence number (seq).
2. Drone receives message and attempts to update the current mission sequence number.
   • On success, the Drone must broadcast a MISSION_CURRENT message containing the current sequence number (seq).
   • On failure, the Drone must broadcast a STATUSTEXT with a MAV_SEVERITY and a string stating the problem. This may be displayed in the UI of receiving systems.

Notes:

• There is no specific timeout on MISSION_SET_CURRENT message.
• The acknowledgment of the message is via broadcast of mission/system status, which is not associated with the original message. This differs from error handling in other operations. This approach is used because the success/failure is relevant to all mission-handling clients.

Monitor Mission Progress

GCS/developer API can monitor progress by handling the appropriate messages sent by the drone:

• The vehicle must broadcast a MISSION_ITEM_REACHED message whenever a new mission item is reached. The message contains the seq number of the current mission item.
• The vehicle must also broadcast a MISSION_CURRENT message if the current mission item is changed.

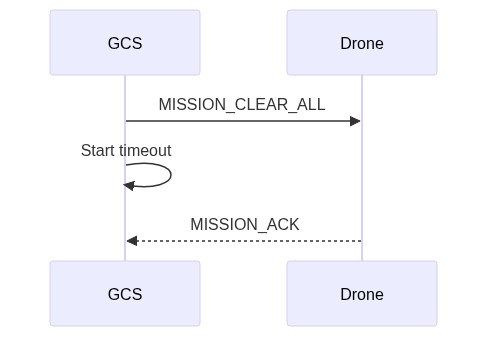
Clear Missions

The diagram below shows the communication sequence to clear the mission from a drone (assuming all operations succeed).

In more detail, the sequence of operations is:

1. GCS/API sends MISSION_CLEAR_ALL
   • A timeout is started for the GCS to wait on MISSION_ACK from Drone.
2. Drone receives the message, and clears the mission from storage.
3. Drone responds with MISSION_ACK with result type of MAV_MISSION_ACCEPTEDMAV_MISSION_RESULT.
4. GCS receives MISSION_ACK and clears its own stored information about the mission. The operation is now complete.

Note:

• A timeout is set for every message that requires a response (e.g. MISSION_CLEAR_ALL). If the timeout expires without a response being received then the request must be resent.
• An error can be signaled in response to any request (in this case, just MISSION_CLEAR_ALL) using a MISSION_ACK message containing an error code. This must cancel the operation. The GCS record of the mission (if any) should be retained.

Canceling Operations

The above mission operations may be canceled by responding to any request (e.g. MISSION_REQUEST_INT) with a MISSION_ACK message containing the MAV_MISSION_OPERATION_CANCELLED error.

Both systems should then return themselves to the idle state (if the system does not receive the cancellation message it will resend the request; the recipient will then be in the idle state and may respond with an appropriate error for that state).

Operation Exceptions

Timeouts and Retries

A timeout should be set for all messages that require a response. If the expected response is not received before the timeout then the message must be resent. If no response is received after a number of retries then the client must cancel the operation and return to an idle state.

The recommended timeout values before resending, and the number of retries are:

• Timeout (default): 1500 ms
• Timeout (mission items): 250 ms.
• Retries (max): 5

Errors/Completion

All operations complete with a MISSION_ACK message containing the result of the operation (MAV_MISSION_RESULT) in the type field.

On successful completion, the message must contain type of MAV_MISSION_ACCEPTED; this is sent by the system that is receiving the command/data (e.g. the drone for mission upload or the GCS for mission download).

An operation may also complete with an error - MISSION_ACK.type set to MAV_MISSION_ERROR or some other error code in MAV_MISSION_RESULT. This can occur in response to any message/anywhere in the sequence.

Errors are considered unrecoverable. In an error is sent, both ends of the system should reset themselves to the idle state and the current state of the mission on the vehicle should be unaltered.

Note:

• timeouts are not considered errors.
• Out-of-sequence messages in mission upload/download are recoverable, and are not treated as errors.

Mission File Formats

The defacto standard file format for exchanging missions/plans is discussed in: File Formats > Mission Plain-Text File Format.

Mission Command Detail

This section is for clarifications and additional information about common mission items. In particular it is intended for cases that are difficult to document in the specification XML, or when images will much better describe expected behaviour.

Loiter Commands (MAV_CMD_NAV_LOITER_*)

Loiter commands are provided to allow a vehicle to hold at a location for a specified time or number of turns, until it reaches the specified altitude, or indefinitely. Multicopter vehicles stop at the specified point (within a vehicle-specific acceptance radius that is not set by the mission item). Forward-moving vehicles (e.g. fixed-wing) circle the point with the specified radius/direction.

The commands are:

• MAV_CMD_NAV_LOITER_TIME - Loiter at specified location for a given amount of time after reaching the location.
• MAV_CMD_NAV_LOITER_TURNS - Loiter at specified location for a given number of turns.
• MAV_CMD_NAV_LOITER_TO_ALT - Loiter at specified location until desired altitude is reached.
• MAV_CMD_NAV_LOITER_UNLIM - Loiter at specified location for an unlimited amount of time, yawing to face a given direction.

The location and fixed-wing loiter radius parameters are common to all commands:

Param (:Label)	Description	Units
3: Radius	Radius around waypoint. If positive loiter clockwise, else counter-clockwise	m
5: Latitude	Latitude
6: Longitude	Longitude
7: Altitude	Altitude	m

The loiter time and turns are set in param 1 for the respective messages. The direction of loiter for MAV_CMD_NAV_LOITER_UNLIM can be set using param4 (Yaw).

INFO

The remaining parameters (xtrack and heading) apply only to forward flying aircraft (not multicopters!)

Xtrack and heading define the location at which a forward flying (fixed wing) vehicle will exit the loiter circle, and its path to the next waypoint (these apply only to apply to only MAV_CMD_NAV_LOITER_TIME and MAV_CMD_NAV_LOITER_TURNS).

Param (:Label)	Description	Units
2: Heading Required	Leave loiter circle only once heading towards the next waypoint (0 = False)	min:0 max:1 increment:1
4: Xtrack Location	Sets xtrack path or exit location: 0 for the vehicle to converge towards the center xtrack when it leaves the loiter (the line between the centers of the current and next waypoint), 1 to converge to the direct line between the location that the vehicle exits the loiter radius and the next waypoint. Otherwise the angle (in degrees) between the tangent of the loiter circle and the center xtrack at which the vehicle must leave the loiter (and converge to the center xtrack). NaN to use the current system default xtrack behaviour.

The recommended values (and resulting paths) are those shown below.

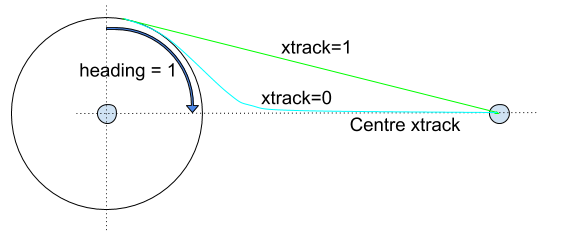
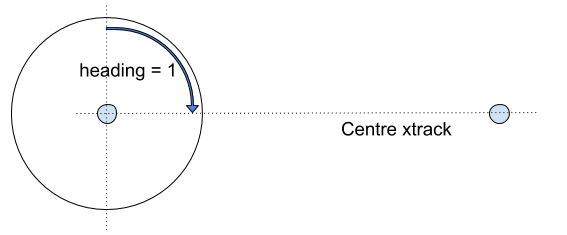
The vehicle leaves the loiter after it reaches the desired number of turns or time and based on both the heading required and xtrack params.

A heading required of 1 prevents the vehicle from exiting the loiter unless it is heading towards the next waypoint (if 0 it can leave at any point provided the other conditions are met). With this setting the vehicle can leave at any point in the arc shown, provided it meets the other conditions (e.g. xtrack). If necessary (i.e. it is not in the arc when the other conditions are met), the vehicle will loop back around the loiter before it evaluates the xtrack condition.

The Xtrack parameter independently defines the path and exit location:

• xtrack=0: Exit the loiter circle and converge to the centre xtrack between this and the next waypoint.

  • If the heading required parameter is not set it will exit the loiter immediately.
  • Otherwise it will leave as soon as it is heading towards the next waypoint (which may also be immediately!)

• xtrack=1: Exit the loiter circle and fly/converge to the straight line between the exit point and the centre of the next waypoint (i.e. don't converge to the centre xtrack).

  • If the heading required parameter is set it will exit the loiter as soon as it is heading towards the next waypoint (which may be immediately!).
  • If the heading required parameter is not set it will exit the loiter immediately (note that this exit path does not make much sense unless the heading parameter is set).

• xtrack=NaN: Exit the loiter using "system specific default behaviour".

  • The vehicle must still respect the heading required param.
  • Usually this is synonymous with xtrack=0

• xtrack=any other value: Exit the loiter when the vehicle heading (tangent) makes the specified angle in degrees to the center xtrack. Converge to the center xtrack. The vehicle must still respect the heading required param (some xtrack values may not be possible with this condition true). This allows callers to specify how quickly the vehicle converges to the center xtrack. For example, the image below shows the vehicle exiting the loiter at 30 degrees.

  

구현

PX4

The protocol has been implemented in C.

Source code:

• src/modules/mavlink/mavlink_mission.cpp

The implementation status is (at time of writing):

• Flight plan missions:
  • upload, download, clearing missions, and monitoring progress are supported as defined in this specification.
• Geofence missions" are supported as defined in this specification.
• Rally point "missions" are not supported on PX4.

Mission operation cancellation works for mission download (sets system to idle). Mission operation cancellation does not work for mission uploading; PX4 resends MISSION_REQUEST_INT until the operation times out.

Source code:

• src/modules/mavlink/mavlink_mission.cpp

QGroundControl

The protocol has been implemented in C++.

Source code:

• src/MissionManager/PlanManager.cc

ArduPilot

ArduPilot implements the mission protocol in C++.

ArduPilot uses the same messages and message flow described in this specification. There are (anecdotally) some implementation differences that affect compatibility. These are documented below.

Source:

• /libraries/GCS_MAVLink/GCS_Common.cpp

Flight Plan Missions

Mission upload, download, clearing missions, and monitoring progress are supported.

INFO

ArduPilot implements also partial mission upload using MISSION_WRITE_PARTIAL_LIST, but not partial mission download (MISSION_REQUEST_PARTIAL_LIST). Partial mission upload/download is not an official/standardised part of the mission service.

ArduPilot's implementation differs from this specification (non-exhaustively):

• The first mission sequence number (seq==0) is populated with the home position of the vehicle instead of the first mission item.
• Mission uploads are not "atomic". An upload that fails (or is canceled) part-way through will not match the pre-update state. Instead it may be a mix of the original and new mission.
• Even if upload is successful, the vehicle mission may not match the version on the uploading system (and if the mission is then downloaded it will differ from the original).
  • There is rounding on some fields (and in some cases internal maximum possible values due to available storage space). Failures can occur if you do a straight comparison of the float params before/after upload.
• A MISSION_ACK returning an error value (NACK) does not terminate the upload (i.e. it is not considered an unrecoverable error). As long as ArduPilot has not yet timed-out a system can retry the current mission item upload.
• A mission cannot be cleared while it is being executed (i.e. while in Auto mode). Note that a new mission can be uploaded (even a zero-size mission - which is equivalent to clearing).
• Explicit cancellation of operations is not supported. If one end stops communicating the other end will eventually timeout and reset itself to an idle/ready state.

The following behaviour is not defined by the specification (but is still of interest):

• ArduPilot performs some validation of fields when mission items are submitted. The validation code is common to all vehicles; mission items that are not understood by the vehicle type are accepted on upload but skipped during mission execution.
• ArduPilot preforms some vehicle-specific validation at mission runtime (e.g. of jump targets).
• A new mission can be uploaded while a mission is being executed. In this case the current waypoint will be executed to completion even if the waypoint sequence is different in the new mission (to get the new item you would need to reset the sequence or switch in/out of auto mode).
• ArduPilot missions are not stored in an SD card and therefore have a vehicle/board-specific maximum mission size (as a benefit, on ArduPilot, missions can survive SD card failure in flight).

Geofence & Rally Point Plans

QGroundControl is the reference implementation for mission / rally point plans.